Veröffentlicht auf Looking Glass Education am 23.05.2023
Originalautor: Daz Bea
Übersetzt von: Sinautoshi am 05.06.2023 - 792979
Dieser Artikel wird auf der Website von European Bitcoiners nur zu Bildungs-, Informations- und Übersetzungszwecken zur Verfügung gestellt und stellt weder eine finanzielle Beratung noch einen Anspruch auf die im Bericht erwähnten Details dar.
Alle Rechte liegen bei dem Autor des Originals.
Das Bitcoin-Protokoll ist in einer Hinsicht ein äußerst komplexes Gebilde. Von der Mathematik der elliptischen Kurve über komplexe Algorithmen und Kryptographie bis hin zu einer Spieltheorie, die selbst den scharfsinnigsten Militärstrategen beeindrucken würde. Einige der tiefgreifendsten Merkmale des Bitcoin-Protokolls, von der fixen Limitierung der Geldmenge, der Halbierung, der Block-Belohnungen und der kontrollierten Versorgung, können durch eine sehr einfache mathematische Formel (Abbildung 1), bekannt als die Bitcoin-Angebotsformel, aufgeschrieben werden.
Bevor wir beginnen, ist es wichtig, den Begriff „Epoche" zu verstehen. Eine Epoche kann für unsere Zwecke einfach als ein beliebiger Zeitraum verstanden werden. Epochen müssen nicht unbedingt genau definiert sein. Ich könnte z.B. einen Langstreckenflug mit 2 Zwischenlandungen als 3 Epochen definieren. Nach der ersten Zwischenlandung kann ich sagen: "Ich befinde mich jetzt in der zweiten Epoche meiner Reise".
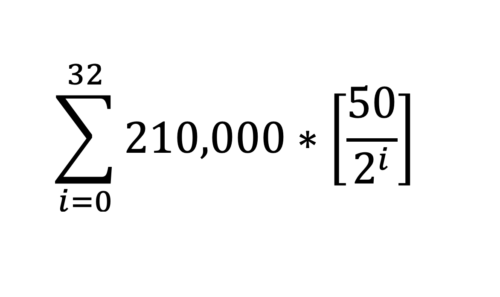
Wenn du in der Schule kein Mathematik studiert hast oder es schon einige Zeit her ist, dass du das getan hast, kann diese Bitcoin-Angebotsformel auf den ersten Blick verwirrend oder sogar ein wenig einschüchternd wirken. Wir sind heute hier, um jeden Teil aufzuschlüsseln und genau zu erklären, was in dieser berühmten Formel vor sich geht.
Wie bereits angedeutet, gibt es in dieser Formel einige Schlüsselzahlen, die mit der Funktionsweise des Bitcoin-Protokolls zusammenhängen.
Lasse uns diese Konzepte, diese Zahlen und ihre Bedeutung vorstellen (Abbildung 2). Wir werden diese einzelnen Zutaten kennen lernen, bevor wir sie zusammenfügen, um den Kuchen zu backen, der die Bitcoin-Angebotsformel ist.
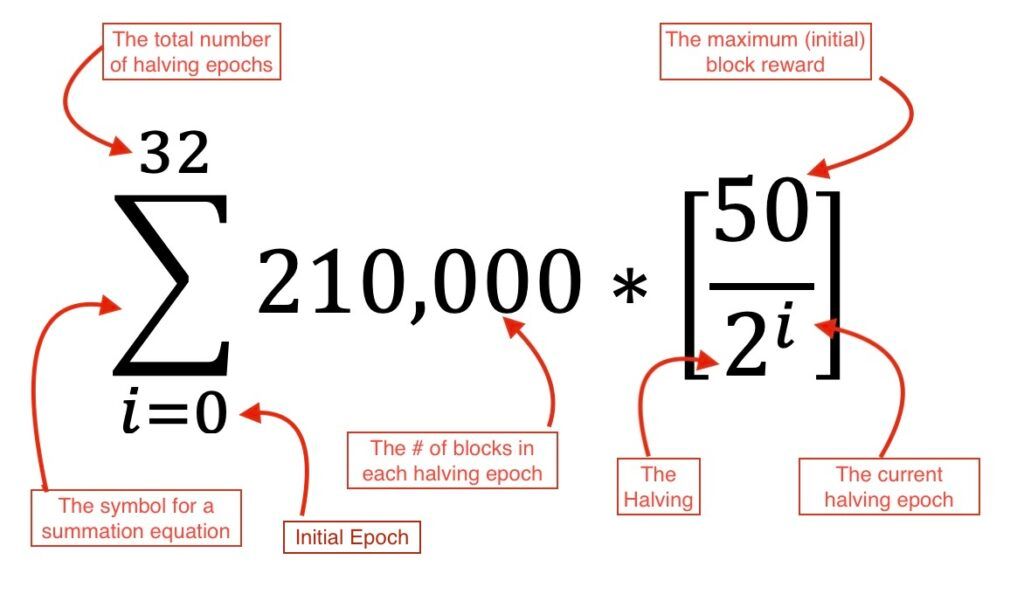
Die Mathematik
Die Bitcoin-Angebotsformel ist eine mathematische Funktion, die als Summationsformel bekannt ist? Was zum Teufel ist eine Summationsformel? Es ist einfach eine Reihe von "+"-Summen. Lass uns einige mathematische Begriffe einführen und dann mit einem einfachen Beispiel fortfahren, um es zu veranschaulichen:
Summationsformeln und Grenzwerte?
∑ (Sigma) - Das Sigma-Symbol (∑) ist das mathematische Symbol für Summation. Dieses Symbol wird in der Regel innerhalb von so genannten Grenzen benutzt.
Die Grenzen - wie bereits erwähnt, sind diese Grenzen, die sich auf unsere Summationsformel beziehen, mathematische Anweisungen, die uns die Grenzen angeben, innerhalb derer wir für unser mathematisches Problem arbeiten müssen. In diesem Fall liegen diese Grenzen zwischen i=0 bis einschließlich i=32. Verwirrt? Ich erkläre es weiter unten.
Um diese neuen Zusammenhänge von Summationsformeln und deren Grenzen zu demonstrieren, beginnen wir mit einer Reihe von einfachen Gleichungen.
Rechne die folgenden Gleichungen nach:

Eine Summationsformel ist so einfach wie das, was wir oben skizziert haben. Eine Reihe von einzelnen Gleichungen, die am Ende alle zusammengerechnet werden.
Aber wie könnten wir dies besser darstellen und kommunizieren, als 3 separate Gleichungen abzutippen?
Benutzen wir die Algebra.
Ich weiß, ich weiß, für einige von euch reicht das Wort Algebra aus, um einen Pickel zu bekommen und ein hohes Maß an Angst auszulösen, wenn ihr euch daran erinnert, wie ihr in der Klasse 10 bei der letzten Matheprüfung geschwitzt habt.
Ehrlich gesagt ist Algebra gar nicht so furchteinflößend, es geht einfach darum, eine Zahl mit Buchstaben zu definieren, die normalerweise als Variable bezeichnet wird. Eine Variable ist einfach eine Zahl, deren Wert wir nicht kennen, oder eine Zahl, die "variieren" kann.
In unseren obigen Gleichungsbeispielen ersetzen wir die zweite Zahl in den Gleichungen durch den Buchstaben "x" und stellen eine Gleichung auf, die wir Gleichung A nennen.

In diesen Fragen war x die Variable, und ihr Wert variierte in jeder Gleichung.
Nun können wir das, was wir oben erreichen wollten, sicherlich noch knapper ausdrücken.
Das können wir, indem wir das Konzept der Grenzwerte verwenden, das wir bereits eingeführt haben. Erstellen wir eine neue Gleichung und formulieren wir, was wir meinen.
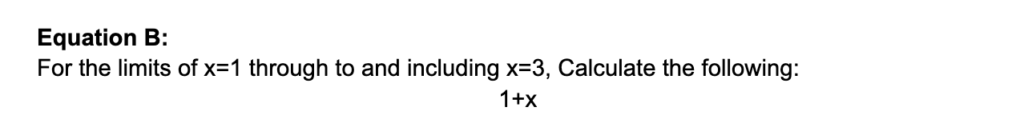
Mit dieser Gleichung gehen wir einfach durch und tun genau das, was wir oben in Gleichung A getan haben, für jeden Wert von x, definiert innerhalb der Grenzen 1 bis 3. Es ist einfach eine andere Art zu schreiben, was wir erreichen wollen.
Wir können dies sogar noch einfacher mit Hilfe der mathematischen Notation ausdrücken. Das sieht dann so aus.
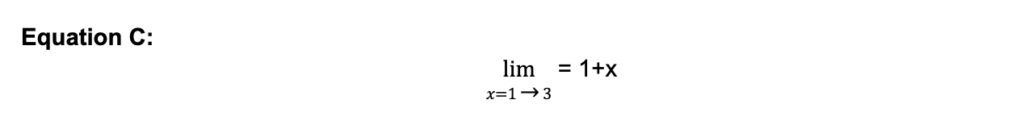
Gleichung C sagt im Grunde genommen: „Ich habe 3 Gleichungen, die du lösen sollst. 1 Gleichung für x=1, eine weitere für x=2 und schließlich eine weitere für x=3. Und die Gleichung, die du lösen sollst, ist 1+x."
Aber das sagt uns nur, dass wir 3 verschiedene Gleichungen aufstellen wollen. Was es uns noch nicht sagt, ist, dass wir sie am Ende alle zusammenzählen wollen.
Wie teilen wir also mit Hilfe der mathematischen Notation mit, dass wir sie auch alle addieren wollen? Wir verwenden das Summengleichungssymbol Sigma (∑).
Wenn wir eine Summationsformel in Kombination mit Grenzwerten verwenden. Die Notation sieht wie folgt aus:
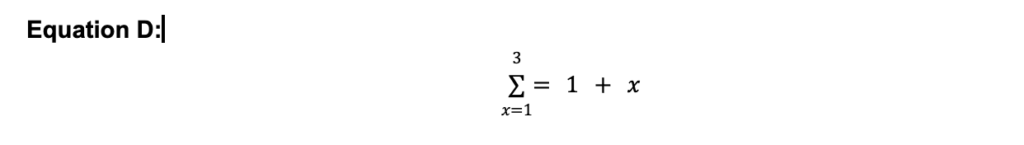
Das bedeutet, dass die Berechnung 1 + x durchgeführt wird, der Wert für x jedes Mal ersetzt wird, wobei der Wert für x jedes Mal von 1 bis einschließlich 3 erhöht wird, und am Ende alle Antworten addiert werden.
Am Ende haben wir eine einzige, hübsche, ordentlich aussehende Gleichung, um das zu vermitteln, was am Anfang drei separate Gleichungen waren, mit einer letzten Gleichung, um alle drei zu addieren.
Siehst du? Ist Mathe nicht schön? Was anfangs ein wenig beängstigend und einschüchternd aussah, war am Ende nur eine Reihe von einfachen Plus(+)-Summen.
Da wir nun ein gutes Verständnis der Symbole und der mathematischen Notation haben, die in der Bitcoin-Versorgungsformel verwendet werden, wollen wir uns nun die einzelnen Zahlen innerhalb der Gleichung ansehen und ihre Bedeutung etwas erläutern. Mach dir keine Sorgen, wenn du anfangs nicht weiter weißt. Wir versprechen, dass sich am Ende alles zusammenfügt.
- i=0 - Dies ist die untere Grenze der Gleichung. Sie steht für die allererste Epoche der Zeit. Als das Bitcoin-Protokoll zum ersten Mal gestaret wurde, befanden wir uns in der ersten Epoche, als i=0 war. Für jede halbierte Epoche wird i um +1 erhöht.
- 32 - 32 ist die Obergrenze für die Gleichung. 32 gibt die Gesamtzahl der Halbierungsepochen an, die innerhalb des Bitcoin-Protokolls auftreten werden. Für jede Halbierungsperiode wird i von 0 (die untere Grenze) bis einschließlich 32 (die obere Grenze) schrittweise erhöht.
- 210.000 - 210.000 ist eine Funktion der Ausgabe neuer Bitcoin, die mit der Anzahl der Blöcke pro Halbierung übereinstimmt. Jeder Zeitraum von 210.000 Blöcken wird als eine Epoche bezeichnet. Nach jeder Epoche von 210.000 Blöcken wird der Grenzwert der Summationsformel (i) um +1 erhöht. Das Bitcoin-Protokoll ist speziell darauf ausgelegt, die Freigabe neuer Blöcke auf einen Durchschnitt von einem Block alle 10 Minuten zu begrenzen. Daher dauert jede Epoche von 210.000 Blöcken etwa 4 Jahre (210.000 x 10 Minuten).
- 50 - Die anfängliche Blockbelohnung während der ersten Epoche der Bitcoin-Geschichte war 50. Wie wir jedoch bald sehen werden, wird diese Zahl in jeder Epoche halbiert.
- 2 - Diese Zahl ist der Grund für den Begriff "Halbierung". Am Ende jeder Epoche wird die Blockbelohnung durch 2 geteilt, mit anderen Worten... sie halbiert sich.
- "i" = Wie oben erwähnt, wird i in der gesamten Summationsgleichung so erhöht, dass es innerhalb der Grenzen der Summationsgleichungen liegt und mit der aktuellen Epoche übereinstimmt. Während der ersten Epoche war i 0 und die Gleichung wird durchgeführt. Während der zweiten Epoche ist i gleich 1 und die Gleichung wird erneut durchgeführt. Wenn wir i in die Gleichung einsetzen, wirkt es wie der Exponent der Zahl 2. Wow!!! Genug der mathematischen Begriffe. Ein Exponent ist ein anderer Begriff für eine Potenz. Beispiel: Wenn i = 3 ist, sehen wir in der Gleichung 23, was im Grunde genommen 2 hoch 3 bedeutet, also 2 x 2 x 2. Wäre i gleich 4, wäre es 2 hoch 4 (24). Das ist eine andere Art zu sagen, dass 2 mit sich selbst 4 mal multipliziert wird, z.B. 2 x 2 x 2 x 2. Der Exponent wirkt sich also direkt auf die Halbierung der initialien Blockbelohnung (die ursprünglich 50 war) in jeder Epoche aus, indem er als Exponent auf die Zahl 2 wirkt.
Fügen wir nun alles zusammen.
Die Bitcoin-Angebotsformel - Die Mathematik
Um unsere Summationsgleichung aufzustellen, gehen wir wie in unseren früheren Beispielen vor. Wir werden alle unsere Gleichungen innerhalb der Grenzen i=0 bis einschließlich 32 durchführen. Dann addieren wir sie alle am Ende. Nochmals zur Formel:
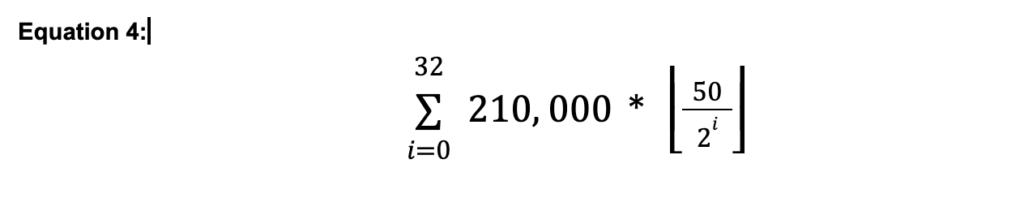
Für den ersten Durchgang setzen wir i=0 in die Gleichung rechts vom Sigma (∑) ein, vervollständigen die Gleichung und notiere dein Ergebnis.
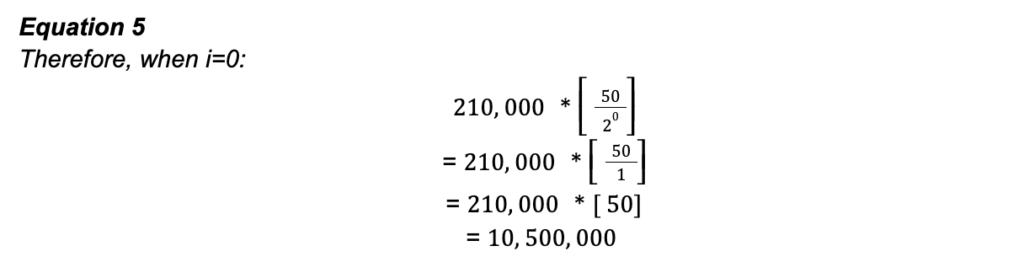
Die Antwort auf diese Berechnung entspricht dem gesamten Bitcoin-Angebot, das während der ersten Epoche der Existenz von Bitcoin (wenn i=0) ausgegeben wurde. 10 500 00 Bitcoin wurden als Belohnung für diejenigen ausgegeben, die ihre Rechenleistung in den Aufbau und die Sicherung der Bitcoin Timechain gesteckt haben.
Sobald die Bitcoin-Timechain eine Blockhöhe von 210.000 Blöcken erreicht hat, erhöht das Protokoll den Wert von "i", damit er mit der nächsten Epoche (wenn i=1) zusammenfällt, und wir führen die Gleichung erneut durch und fügen sie zu unserem bestehenden Ergebnis hinzu.

Wie wir oben sehen können, wurden während der zweiten Epoche, in der i=1 ist, angesichts der Tatsache, dass die Blockbelohnung von 50 in der ersten Epoche (wenn i=0) auf 25 während der zweiten Epoche (wenn i=1) gesunken ist, nur 5 250 000 Bitcoin gemined.
Wir können nun die Angebotsausgabe aus beiden Epochen addieren, um zu sehen, wie viele Bitcoin nach der zweiten Epoche im Umlauf waren.
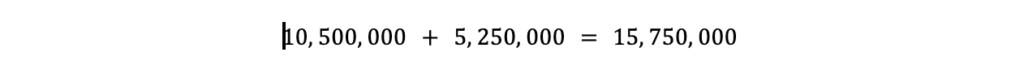
Wenn wir zur 3. Epoche übergehen, erhöhen wir einfach i um +1 und führen die Gleichung erneut durch, wobei wir die Summen aus jeder Epochenberechnung addieren.

Jetzt sollten wir das Muster erkennen: Beim Übergang zu jeder Epoche wird i um +1 erhöht, und wir führen die Berechnung der Ausgabe für jede Epoche von 210.000 Blöcken durch.
Wir sollten nun auch verstehen, wie die Blockbelohnung jedes Mal halbiert wird, wenn i erhöht wird. In der ersten Epoche hatten wir eine Blockbelohnung von 50, in der zweiten von 25 und in der dritten von 12,5. Und so geht es weiter bis zur letzten Epoche, wenn i=32.
In jeder Epoche werden die Blockbelohnungen halbiert. Daher verwenden wir den Begriff Halving (Halbierung). Während wir mit jeder Epoche fortfahren, wird der Exponent "i" in der Gleichung weiterhin auf die Blockbelohnung einwirken und sie jedes Mal halbieren, bis wir die obere Grenze unserer Summationsgleichung erreichen, wenn i=32 ist.
Nun können wir jede Gleichung nacheinander durchführen und unsere Ergebnisse berechnen, bis wir die letzte Epoche mit der Obergrenze von i=32 erreichen. Wir können dies manuell tun oder einen Taschenrechner, eine Excel-Tabelle oder ein Online-Mathe-Tool verwenden, um die schwere Arbeit zu erledigen.
Zur Veranschaulichung verwenden wir Excel, um den Rest unserer Arbeit zu erledigen (Abbildung 3).
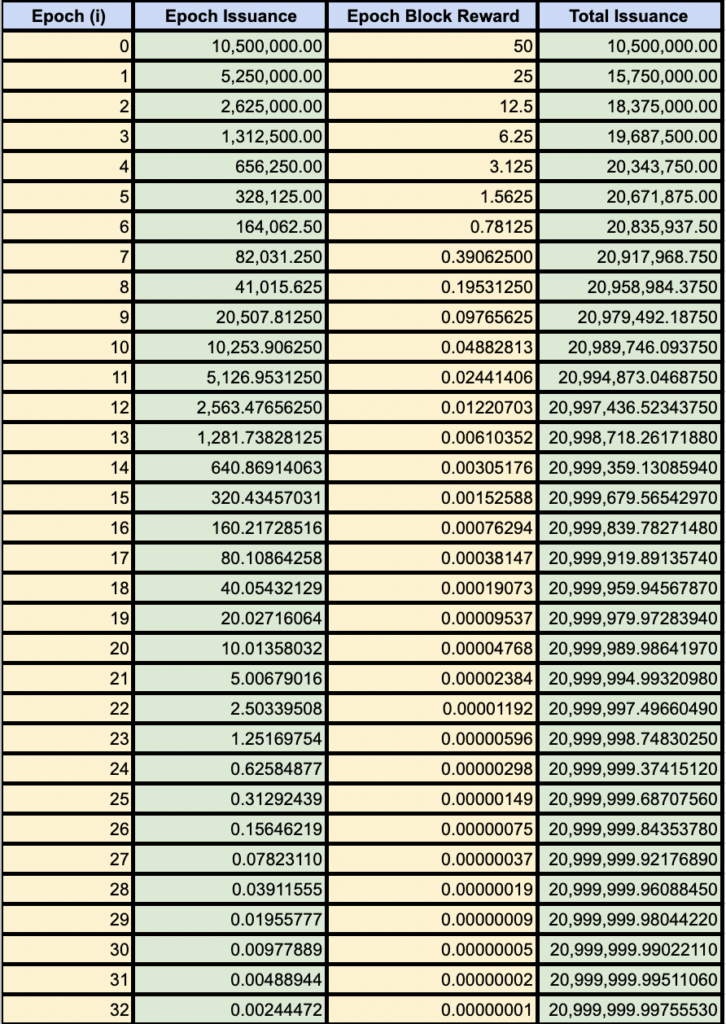
Wenn du die Zahlen in Abbildung 3 betrachtest, fällt dir vielleicht etwas auf. Wir sprechen oft davon, dass Bitcoin eine feste Angebotsobergrenze von 21 000 000 (Millionen) Bitcoin hat. Wenn du dir jedoch die Zeit nimmst, die Berechnungen anzuschauen, sehen wir, dass wir das Ziel eigentlich nie ganz erreichen. Wir erreichen 21 000 000 Bitcoin nur knapp, ~ 244 470 Satoshi fehlen.
Hoffentlich hast du jetzt ein besseres Verständnis dafür, wie die Bitcoin-Angebotsformel funktioniert, und hast vielleicht sogar ein paar mathematische Spinnweben auf dem Weg dorthin abgestreift.
Vielen Dank fürs Lesen.
Die Zukunft wird rosig dank Bitcoin.

Sinautoshi
#Bitcoin only - #GetOnZero - united we fix the money (supply to 21M BTC)
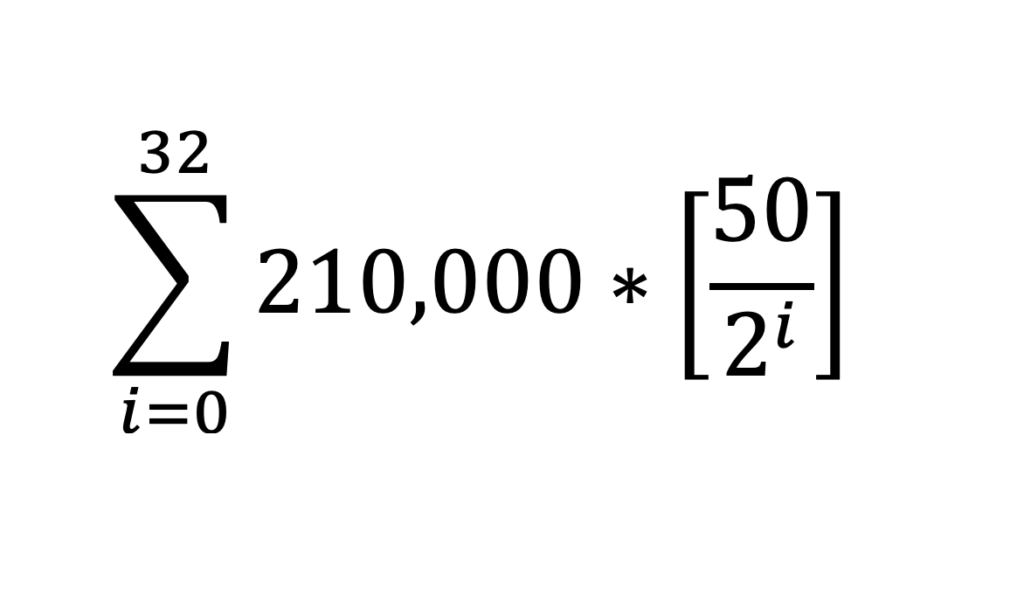



Related Posts
Neujahrsgruß 2026: 12k-Basti und die letzte Fiat-Illusion
Jan 01, 2026
Die Plebs die Bitcoin zum Leuchten bringen
Dec 28, 2025
Bitcoin als zeitabhängiger Potentialtopf: Eine physikalische Analyse der Hyperbitcoinisierung durch die Linse der Proteinfaltung
Aug 10, 2025