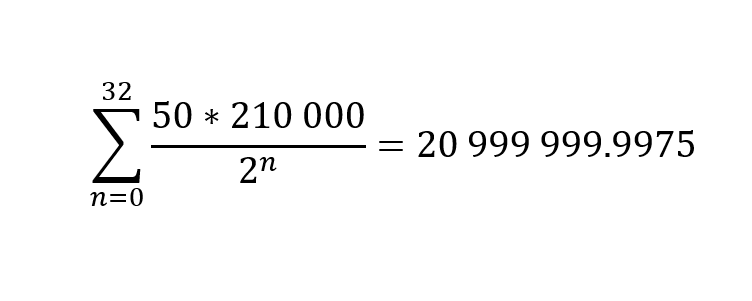Autore: Daz Bea | Pubblicazione originale: 23 mag 2023 | Tradotto da: 31febbraio | Milano Trustless | Link: The Bitcoin Supply Formula – Explained
l protocollo bitcoin, da un certo punto di vista, è una bestia estremamente complessa. Dalla matematica della curva ellittica, agli algoritmi complessi, alla crittografia, agli strati di teoria dei giochi che impressionerebbero il più astuto degli strateghi militari. Alcune delle caratteristiche più profonde del protocollo bitcoin, dal tetto massimo di fornitura, all'halving, alle ricompense dei blocchi e all'emissione di forniture, possono essere comunicate da una formula matematica molto semplice (Figura 1) nota come Bitcoin Supply Formula - formula che regola l'emissione di bitcoin.
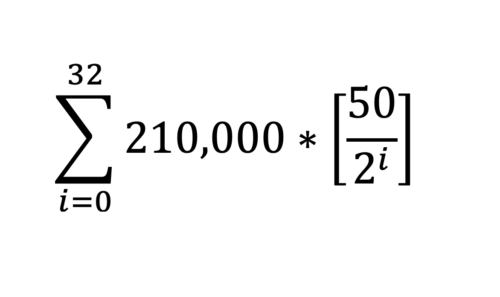
Se non avete studiato matematica a scuola, o se è passato un po' di tempo dall'ultima volta che l'avete fatto, a prima vista questa formula dell'emissione di bitcoin può sembrare confusa o addirittura un po' intimidatoria. Oggi siamo qui per analizzare ogni parte e spiegare esattamente cosa succede in questa famosa formula.
Come accennato in precedenza, all'interno di questa formula esistono alcuni numeri chiave relativi al funzionamento del protocollo bitcoin.
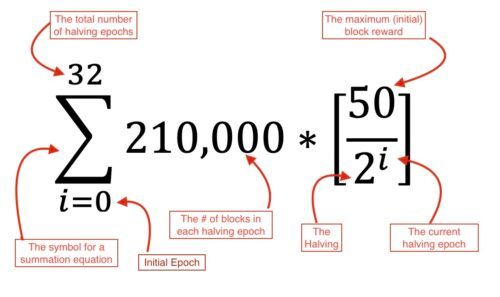
Introduciamo questi concetti, questi numeri e il loro significato (Figura 2). Studieremo questi singoli ingredienti prima di metterli insieme per preparare la ricetta finale, che è la formula dell'emissione monetaria di bitcoin.
La matematica
La formula dell'emissione di bitcoin è una funzione matematica nota come sommatoria. Cosa diavolo è una sommatoria? È semplicemente una serie di somme '+'. Introduciamo alcuni termini matematici e proseguiamo con un semplice esempio per illustrare il tutto:
Sommatorie e Limiti?
∑ (Sigma) - Il simbolo Sigma (∑) è il simbolo matematico della sommatoria. Questo simbolo viene solitamente comunicato all'interno di quelli che chiamiamo Limiti.
I limiti - come già detto, in relazione alla nostra sommatoria, sono istruzioni matematiche che ci indicano i limiti entro i quali dobbiamo lavorare per il nostro calcolo. In questo caso i limiti sono compresi tra i=0 fino a i=32 incluso.
Confusi? È più chiaro di seguito.
Per dimostrare questi nuovi concetti di sommatoria e limiti, iniziamo con una serie di semplici equazioni.
Svolgiamo le seguenti equazioni:

Una sommatoria è semplice come quella che abbiamo descritto sopra: una serie di singole equazioni che si sommano alla fine.
Ma come possiamo rappresentarla e comunicarla meglio, invece di dover digitare 3 equazioni separate?
Utilizzando l'algebra.
Lo so, lo so, per alcuni di voi la parola Algebra è sufficiente a far venire i brufoli e a scatenare alti livelli di ansia, mentre ricordate di aver sudato per l'esame di matematica dell'ultimo anno.
In realtà, l'algebra non è così spaventosa: si tratta semplicemente di usare delle lettere per definire un numero, solitamente descritto come variabile. Una variabile è semplicemente un numero di cui non conosciamo il valore, o un numero che può 'variare'.
Negli esempi di equazioni precedenti, sostituiamo il secondo numero dell'equazione con la lettera 'x', per creare un'unica equazione, che diventa l'equazione A.

In queste formule, x è una variabile e il suo valore varia in ogni equazione.
Possiamo comunicare in modo ancora più sintetico ciò che volevamo ottenere sopra? È sicuramente possibile, utilizzando il concetto introdotto in precedenza, quello dei limiti. Creiamo una nuova equazione per spiegare cosa intendiamo.
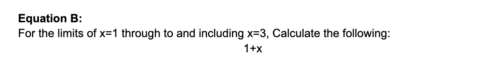
Con questa equazione, ci limitiamo a fare esattamente come abbiamo fatto sopra nell'equazione A, per ogni valore di x, definito entro i limiti da 1 a 3. È semplicemente un modo diverso di comunicare ciò che vogliamo ottenere.
Possiamo comunicarlo in modo ancora più semplice utilizzando la notazione matematica. In realtà si presenta così.
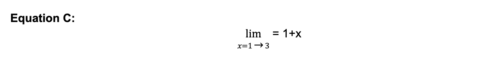
L'equazione C sta effettivamente dicendo: 'Ho 3 equazioni che voglio che tu faccia. Un'equazione per quando x=1, un'altra per quando x=2 e infine un'altra per quando x=3. E l'equazione che voglio che tu esegua è 1+x'.
Ma questo ci dice solo che vogliamo fare 3 equazioni separate. Non ci dice ancora che vogliamo sommarle tutte alla fine.
Quindi, come facciamo a comunicare con la notazione matematica che vogliamo che anche voi le sommiate? Usiamo il simbolo della Sommatoria, Sigma (∑).
Quando usiamo una sommatoria, combinata con i limiti, la notazione si presenta come segue: ∑ 'Sigma'. La scrittura si presenta in questo modo:
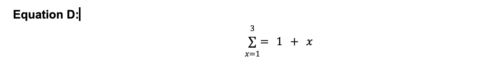
Ciò significa che
- si esegue il calcolo 1 + x
- si sostituisce il valore di x ogni volta, incrementando il valore di x ogni volta, con i valori compresi tra 1 e 3
- per poi sommare tutti i risultati alla fine.
Al termine si ottiene un'unica equazione, bella e ordinata, per comunicare quelle che all'inizio erano 3 equazioni separate, con un'equazione finale per sommare tutte e 3 le risposte.
Non è bella la matematica? Quello che all'inizio sembrava un po' spaventoso e intimidatorio, alla fine si è rivelato solo una serie di semplici somme di addizioni (+).
Ora che abbiamo una buona comprensione dei simboli e delle notazioni matematiche utilizzate nella Bitcoin Supply Formula, analizziamo i singoli numeri all'interno dell'equazione e diamo un po' di colorito al loro significato. Non preoccupatevi se all'inizio vi perdete. Alla fine tutto torna, promesso.
- i=0 - È il limite inferiore dell'equazione. Rappresenta l'epoca iniziale del tempo. Quando il protocollo bitcoin è stato scoperto per la prima volta, ci trovavamo nella prima epoca, quando i=0. Per ogni epoca di halving, i viene incrementato di +1:
- 32 - 32 è il limite superiore dell'equazione. 32 indica il numero totale di epoche di halving che si verificheranno nel protocollo. Per ogni periodo di dimezzamento, i viene incrementato da 0 (il limite inferiore) fino a 32 (il limite superiore);
- 210.000 - 210.000 è una caratteristica della funzione che regola l'emissione di nuovi bitcoin. Coincide con il numero di blocchi per ogni halving/dimezzamento. Ogni periodo di 210.000 blocchi viene definito Epoca. Dopo ogni epoca di 210.000 blocchi, il limite dell'equazione di somma (i) viene aumentato di +1. Il protocollo bitcoin è specificamente progettato per controllare il tasso di emissione di nuovi bitcoin, a una media di un blocco ogni 10 minuti. Sono quindi necessari circa 4 anni (210.000 x 10minuti) per ogni epoca di 210.000 blocchi;
- 50 - l'iniziale ricompensa di blocco durante la prima epoca della vita di bitcoin era di 50 BTC. Tuttavia, come vedremo tra poco, questo numero si dimezza ad ogni epoca:
- 2 - da questo numero deriva il termine 'halving', il dimezzamento. Alla fine di ogni epoca, la ricompensa diblocco viene divisa per 2, in altre parole... si dimezza;
- 'i' = come già detto, in tutta la sommatoria i viene incrementato per rientrare nei limiti dell'equazione e per coincidere con l'epoca corrente.
Cosa succede nella pratica: durante la prima epoca, i=0 e si esegue l'equazione, ottenendo il risultato. Durante la seconda epoca, i=1 --> di nuovo si esegue l'equazione. Quando si sostituisce i nell'equazione, questa variabile diventa l'esponente del numero 2. Wow! Basta con i termini matematici. L'esponente è un altro termine per indicare la potenza [l'elevamento a potenza]. Esempio: Quando i = 3, nell'equazione vediamo 23, che in pratica significa 2 elevato alla potenza di 3, ovvero 2 x 2 x 2. Analogamente, se i=4, diventa 2 elevato alla quarta (24). Che è un altro modo per dire 2 moltiplicato per se stesso 4 volte, ad esempio 2 x 2 x 2 x 2. L'esponente, quindi, influisce direttamente sul dimezzamento della ricompensa iniziale del blocco (che inizialmente era 50) a ogni epoca, agendo come esponente sul numero 2.
Dopo aver esposto tutto questo, vediamo di mettere insieme tutte le parti.
Fare i conti - La formula della fornitura di Bitcoin
Per eseguire la nostra sommatoria, faremo come negli esempi precedenti. Eseguiremo tutte le equazioni entro i limiti da i=0 a i=32 incluso. Poi le sommeremo tutte alla fine. Rivediamo di nuovo la formula:
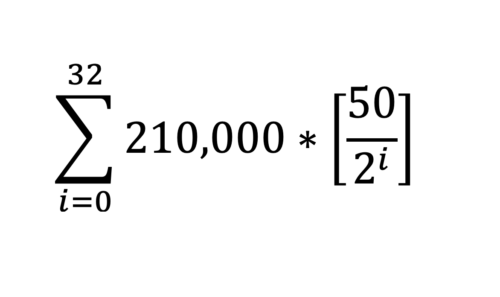
Per il primo passaggio, sostituiamo i=0 nell'equazione a destra di (sommatoria) ∑, completiamo l'equazione e calcoliamo il risultato.
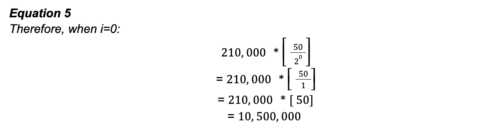
La risultante di questo calcolo, corrisponde all'emissione totale di bitcoin durante la prima epoca di esistenza di bitcoin (quando i=0, cioè dal 3/1/2009 al 28/11/2012). Come ricompensa a coloro che hanno scelto di destinare la loro potenza di calcolo alla costruzione e alla sicurezza della Timechain di bitcoin, sono stati rilasciati un totale di 10.500.00 di bitcoin.
Ora, seguendo le regole dell'equazione di somma, una volta che la timechain di bitcoin ha raggiunto un'altezza di altri 210.000 blocchi (nota come Block-Height), il protocollo ha incrementato il valore di 'i' in modo da farlo coincidere con l'epoca successiva (quando i=1), e noi eseguiamo nuovamente l'equazione, aggiungendolo al nostro risultato.
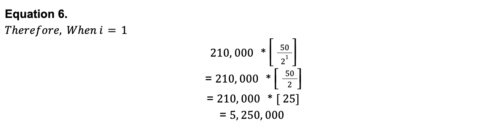
Come possiamo vedere sopra, durante la seconda epoca, dove i=1, dato che la ricompensa del blocco è diminuita da 50 nella prima epoca (quando i=0) a 25 durante la seconda epoca (quando i=1), sono stati estratti solo 5.250.000 bitcoin.
Possiamo ora sommare l'emissione di offerta da entrambe le epoche per vedere quanti bitcoin erano in circolazione dopo la seconda epoca.
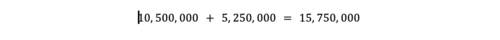
Quando si passa alla terza epoca, è sufficiente incrementare i di +1 e ripetere l'equazione, continuando a sommare i totali dell'emissione di bitcoin che avvengono in ogni epoca.

Iniziamo a vedere lo schema: quando passiamo a ogni epoca, i viene incrementato di +1 e si esegue il calcolo dell'emissione per ogni epoca di 210.000 blocchi.
Iniziamo anche a capire come la ricompensa dei blocchi si dimezzi ogni volta che i viene incrementato. Siamo passati da una ricompensa pari a 50 bitcoin durante la prima epoca, a 25 nella seconda, a 12,5 nella terza. E questo continuerà fino all'ultima epoca, quando i=32.
A ogni epoca le ricompense dei blocchi vengono dimezzate. Per questo motivo è stato coniato il termine 'halving', dimezzamento. Man mano che proseguiamo in ogni epoca, l'esponente 'i' nell'equazione continuerà ad agire sulla ricompensa dei blocchi, dimezzandola ogni volta fino a raggiungere il limite superiore della sommatoria, quando i=32.
A questo punto, possiamo continuare a eseguire ogni equazione una alla volta, calcolando i risultati fino a raggiungere l'epoca finale con il limite superiore di i=32. Possiamo continuare a farlo manualmente, oppure utilizzare una calcolatrice, un foglio di calcolo o uno strumento matematico online per fare il lavoro pesante.
Per dimostrarlo, usiamo un foglio di calcolo per fare il resto del lavoro (Figura 3).
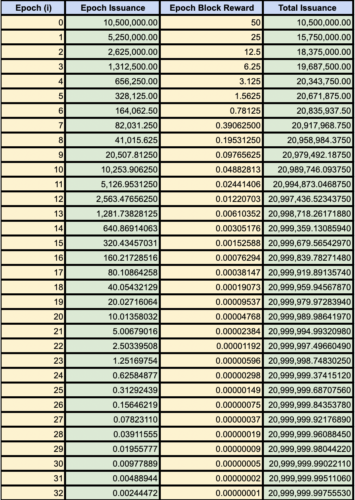
Studiando i numeri della Figura 3 si può notare qualcosa. Spesso si parla di bitcoin come di un limite di offerta fisso di 21.000.000 di monete. Se ci si prende il tempo di fare i calcoli, però, si può vedere che, in realtà, non ci si arriva mai. Arriviamo appena al di sotto di 21.000.000 di circa ~244.470sat.
Si spera che ora sia più chiaro come funziona la Bitcoin Supply Formula e che magari, lungo la strada, abbiate anche tolto qualche ragnatela dai ricordi di matematica.
Per un'immersione più approfondita nei meccanismi alla base di bitcoin, si consiglia di consultare il libro: B is for Bitcoin, disponibile sia in formato cartaceo che ebook negli store online
 European BitcoinersMilano Trustless (31febbraioMI)
European BitcoinersMilano Trustless (31febbraioMI)
 European BitcoinersMilano Trustless (31febbraioMI)
European BitcoinersMilano Trustless (31febbraioMI)